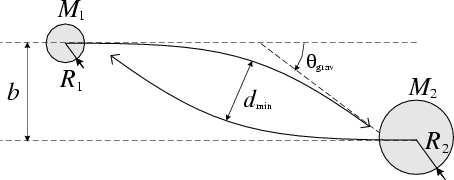
We now introduce some quantities and definitions for the pages on stellar collisions.
We consider collisions between two stars, originaly unbound to each other and neglect the gravitational influence of other bodies in the cluster. Letting aside the details of the stellar structure, which play an obvious role in determining the outcome of a collision and its significance in a given astrophysical context, the initial conditions of a collisions are completely described by 4 quantities: the stellar masses, M_1 and M_2 (usually in units of the sun’s mass, M_sun), the impact parametre b (see diagram) and the relative velocity of the stars at infinity, V_rel. Of course, in order to know whether a collision will happen at all, we need to know the stellar radii, R_1 and R_2 (usually in units of the sun’s mass, R_sun). If the stars where point masses, their trajectories would be Keplerian hyperbolae, with pericenter distance d_min and deflection angle theta_grav.
From simple energy and angular momentum considerations, one gets:
where V_star is the relative at contact if the stars were initially at rest at infinity:
The velocity is typically of order 500-1000 km/s for collision between MS star, or a MS star and a more compact star.A collision occurs when the centers of the stars are closer to each other than d = eta*(R_1+R_2). If we neglect tidal deformations (OK for high speed collisions), eta=1 for genuine collision. At small relative velocities, tidal captures may occur, which corresponds to eta>1. Note that the fate of tidally formed binaries is a complicated problem but it is likely that, in many cases, the stars will eventually merge. Hence, tidal captures should always be included when one discuss collisions (unless the velocity dispersion is high enough to suppress them).
The cross-section for encounters with closest approach smaller or equal to d (neglectig tidal perturbations of the Keplerian trajectories) is:
The second term in the large brackets is the “gravitational focusing”, which. It dominates if V_rel << V_ast (for eta=1), which is the case in globular clusters (velocity dispersions of a 10-20 km/s) or open clusters (1 km/s or less). In this case,
Note that the cross section scales linearly with the closest approach distance so that all values of d_min, from 0 to eta*(R_1+R_2) have equal probability. This is not so if V_rel >> V_ast, which is the case in the center-most part of galactic nuclei, where a massive black hole impose very high velocities. In this case, the cross section is simply geometrical and the probability of having closest approach d_min is proportional to d_min. Hence, (near) haed-on collisions are very unlikely.The regime with V_rel << V_ast is refered as parabolic. V_rel play little role in the hydrodynamics of genuine collisions (with contact at first peri-center passage), but it is crucial to determine the critical d_min (> R_1+R_2) for tidal captures. Such collisions are only mildly supersonic as the thermal velocity of the stellar gas is of order V_ast which is also approximately the relative velocity at contact.