Semi-analytical methods
Two classes of methods have been developed that aim at ‘guessing’ the result of a stellar collision without resorting to an explicit hydrodynamical simulation. So far they have been applied only for MS–MS collisions.
- Spitzer & Saslaw model (high velocity collisions)
- Lombardi’s fluid sorting (low velocity collisions)
The hope is to get a semi-analytical method to get detailed prediction about the outcome of collisions (masses, velocities and stellar structure(s)) with only a tiny fraction of the computational burden of full-fledged hydrodynamical simulations. Indeed, even with a relatively low resolution (of order 10000 particles), an SPH simulation requires at least a few hours of CPU time on a standard PC. It is thus clear that incorporating ‘live’ hydrodynamics into stellar dynamical simulation is still not an option, except maybe for the slowest stellar dynamics schemes (i.e. direct N-body) and for clusters in which collisions are rare.
1. Spitzer & Saslaw model
In a pioneering work about the collisional dynamics of dense proto-galactic nuclei, Spitzer & Saslaw (1966) introduced a simple, semi-analytical model to determine the outcome (mass and energy loss) of high speed stellar collisions. This approach has been applied by David, Durisen & Cohn (1987a,1987b) and extended to unequal mass collisions by Sanders (1970) and by Murphy, Cohn & Durisen (1991).
 Figure taken from Murphy, Cohn & Durisen (1991).
Figure taken from Murphy, Cohn & Durisen (1991).
The computation preceeds as follows. The colliding stars are decomposed into a lrage number of sticks, parallel to the direction of the relative motion. It is assumed that, from the time of first contact, the collision proceeds on a straight trajectory. In the overlapping regions of the stars, one considers conservation of momentum and energy (including thermal energy) in individual encounters between one stick from the fisrt star and one stick from the other (in black on the figure). No transverse energy or momentum transfer is taken into account. If, after the collision, the total specific energy of a stick relative to its parent star is higher than the binding energy, G*M_star/R_star, this element of mass is considered lost from the parent star (of mass M_star and radius R_star).
Although quite crude, this model gives results for the mass lost in surprisingly good agreement with SPH simulations when the relative velocity at infinity is larger than the stellar escape velocity and the impact parameter is relatively large, d_min>0.4*(R_1+R_2).
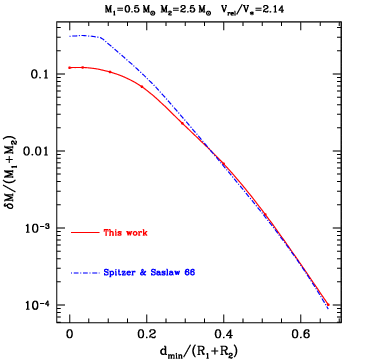 Figure: comparison of the fractional mass loss between SPH simulations by Freitag (Freitag 2000, Freitag & Benz 2002) and the Spitzer & Saslaw semi-analytical model applied to the same stellar models.
Figure: comparison of the fractional mass loss between SPH simulations by Freitag (Freitag 2000, Freitag & Benz 2002) and the Spitzer & Saslaw semi-analytical model applied to the same stellar models.
This regime corresponds to most likely collisions in the centre-most parts of a galactic nucleus where a central massive black hole imposes high velocities. Future work, in particular detailed comparisons with hydrodynamical simulations, will tell us if it can be used to determine the entropy of gas elements in order to predict the post-collisional stellar structure, in conjunction with some fluid sorting algorithm, and if an extension of this method can be devised for the regime of intermediate velocities (V_rel of order of V_star) and/or small impact parameters.
2. Lombardi’s fluid sorting
If the relative velocity at infinity, V_rel, is lower than the stellar escape velocity, V_star (of order 500-1000 km/s), which is the case for collisions happening in open or globular clusters, the relative velocity at contact is similar to the thermal velocity of stellar matter. Hence, such collisions are only mildly supersonic and entropy is nearly conserved. Consequently, the structure of the merger can be established by sorting the mass elements from the parent stars according to their entropy, as demonstrated by Lombardi and his collaborators (Lombardi et. al. 2002).
Make Me A Star (MMAS) is a freeely available software package that quickly generates collision product models for such scenarios. MMAS implements fast fluid-sorting algorithms to treat nearly parabolic encounters between low-mass main sequence stars, including an approximate treatment of mass loss and shock heating. This software is intended to be used in combination with realistic dynamical simulations of star clusters.
You can clone the most updated version of mmas here
$ git clone git@github.com:pau-amaro-seoane/mmas.git
MMAS is currently being implemented as the hydrodynamics module of two on-line programs that unite stellar dynamics, hydrodynamics and evolution:
TRIPTYCH is a computer program that simulates the collision of two stars, including the orbital trajectories, merger, and evolution of the merger product. You can clone the most updated version of project on the following github:
$ git clone git@github.com:pau-amaro-seoane/triptych.git
An outgrowth of TRIPTYCH is a sister program, called TRIPLETYCH, that simulates the interaction of three stars, including the orbital trajectories, possible merger(s), and the subsequent evolution of the merger product. TRIPLETYCH can also be run online via a web interface. To start the simulation the user must choose the parent stars involved, set the velocity at infinity and impact parameter of the outer orbit, and set the semi-major axis and eccentricity of the inner orbit. All other orbital parameters are chosen at random (but the random seed may be specified to allow reproducible results).
McMillan has implemented the stellar dynamics of the three parent stars in TRIPLETYCH using the scatter3 routine from STARLAB, with visualizations generated by the snap_to_image routine. Two of the stars are initially bound, with the third approaching from infinity. The scattering package is described in detail by McMillan & Hut (1996). All orbital parameters may be specified by the user; those left unset are chosen randomly from appropriate distributions.
All STARLAB scattering packages (scatter3 and its higher-order generalizations) compute an encounter until it is unambiguously over–that is, two “stable” objects are receding from one another with positive velocity at infinity. A stable object is a star or merger product, or any binary or dynamically stable multiple whose components are themselves stable. Within TRIPLETYCH, the software automatically detects collisions and close encounters, classifies the dynamical state of the system, and passes all data to the stellar hydrodynamics module. Currently, the dynamical calculation is resumed (via a simple Kepler solver in the three-body case, or by reverting to the scattering package in more complex configurations) once dynamical equilibrium is restored, as determined by MMAS. Should a second collision occur, the structure of the new triple merger product is computed similarly.
Once no further interactions are indicated, a stellar evolution module developed by Hurley is employed to determine the long-term evolution of the resulting object(s). The separation of functionality just described is consistent with the characteristic time scales expected for the dynamical, hydrodynamical, and stellar-evolutionary processes involved in a simple three-body scattering. However, for more complex interactions, it will probably be desirable to integrate the three modules more closely, for example using the stellar evolution interfaces defined in MODEST-1 and implemented in TRIP(LE)TYCH by Hurley, including equivalent prescriptions for the evolution of newly merged systems not yet in thermal equilibrium.
Smoothed Particle Hydrodynamics (SPH)
Smoothed Particle Hydrodynamics is a Lagrangian particle-based method that has been widely used to tackle all kinds of astrophysical problems, from planetesimal fragmentation to cosmological structure formation. For a description of the method and of its achievements, we refer to reviews by Benz (1990), Monaghan (1992,1999,2001) or Rasio (1999). Peter J. Cossins has written a chapter of his thesis reviewing the subject (2010). For a minimalist introduction to SPH, taken from Freitag (2000), follow this link.SPH simulations of stellar collisionsSPH codes do not impose any restriction on the geometry of the problem, are best suited for highly dynamical situations (rather than quasi-hydrostatic ones), adapt naturally to a wide range of spatial scales and don’t waste computational resources on void spaces. For all these reasons, SPH is particularly well suited to the simulation of stellar collisions. And indeed, most investigations in that field were done using SPH, as this (incomplete) list of SPH collision simulation papers testifies:
The SPH method was invented in 1977 independently by Gingold & Monaghan and Lucy to study the fission of rotating (proto)stars. In 1979, it was applied to investigate the disruption of a star due to the tidal pull of a companion (Gingold & Monaghan 1979). SPH simulations of collisions between interstellar gas clouds were done in 1985 by Lattanzio et al. and, in 1986 Benz et al. considered the collision between the proto-earth and a large object to explain the origin of the moon. The first published SPH simulations of stellar collisions are the ones by Benz & Hills (1987). The field has since grown to a small industry and keeping track of all publications is difficult.
An SPH code designed for stellar collisions is StarSmasher, initially developed by F. Rasio and later by James Lombardi and many others. You can clone the latest version on github:
$ git clone https://github.com/jalombar/starsmasher.git
The code is mostly meant to be run on NVIDA GPUs but there is a CPU version of it. The scheme is a Lagrangian particle one that approximates a continuous fluid as discrete nodes, each carrying various parameters such as mass, position, velocity, pressure, and temperature. In an SPH simulation the resolution scales with the particle density, and StarSmasher is able to handle both equal-mass and equal number-density particle models.
StarSmasher solves for hydro forces by calculating the pressure for each particle as a function of the particle’s properties – density, internal energy, and internal properties (e.g. temperature and mean molecular weight). The code now implements variational equations of motion and libraries to calculate the gravitational forces between particles using direct summation on NVIDIA graphics cards. Using a direct summation instead of a tree-based algorithm for gravity increases the accuracy of the gravity calculations at the cost of speed. The code uses a cubic spline for the smoothing kernel and an artificial viscosity prescription coupled with a Balsara Switch to prevent unphysical interparticle penetration. The code also implements an artificial relaxation force to the equations of motion to add a drag term to the calculated accelerations during relaxation integrations.
SPH references for stellar collisions
Here is an incomplete list, organized by collision type. In this table q stands for the mass ratio M_2/M_1; other quantities are defined here.
| Collision type and regime | References |
|---|---|
| Proto-stars | Lin et al 1998 (collisions between proto-stellar disks) Zinnecker & Bate 2002 (conference proceeding discussing collisions between pre-MS stars in a young cluster; show how a low-mass star can be tidally disrupted by a more massive star) Laycock & Sills 2005 (collisions between a pre-MS star and a variety of other stars) Davies et al, 2006 (collisions involving pre-MS stars; discussion of how they may contribute to massive-star formation in young clusters) |
| MS — MS low velocity | Lombardi, Rasio & Shapiro 1995,1996 (blue straggler formation; q=0.2-1) Sandquist, Bolte & Hernquist 1997 (Study of the mixing during merger and blue straggler evolution) Sills et al. 1997,2001 (SPH simuls to investigate structure and evol. of blue stragglers; up to Np=1e5) Barnes 2000 (comparison with collision of galaxies; polytropes n=1.5; q=0.5/1) Lombardi et al. 2002 (SPH simuls to validate semi-analytical model) Sills et al. 2002 (up to Np=1e6 to determine blue straggler structure) Lombardi et al. 2003 (Triple collisions, SPH simuls used to demonstrate applicability of fluid sorting method) Sills, Adams & Davies 2005 (Concentrate on effect of rotation on structure and evolution of blue straggler) Dale & Davies 2006 (Collisions involving massive stars; discuss evolution of collision product in context of GRB and formation of very massive stars) Suzuki et al. 2007 (Collisions involving massive stars and evolution of merger product in the context of “runaway” growth of very massive stars in clusters) Trac, Sills & Pen 2007 (Comparison between SPH and grid code [TVD] for equal-mass, 0.8 Msun collisions) Gaburov et al. 2007 (Collisions involving massive stars; extend and test fluid sorting algorithm for this regime) |
| MS — MS high velocity | Benz & Hills 1987 (polytropes n=1.5; Np=1000; q=1; 0-2.33*V_star) Benz & Hills 1992 (polytropes n=1.5; Np=7000; q=.2; 0-5*V_star) Lai, Rasio & Shapiro 1993 (Eddington models, n=3; Np=8000; q=0.1-1; 0.2-3.8*V_star) Rauch 1999 (simul. by M. Davies) (polytropes n=3; q=0.25-1; 1-25*V_star) Freitag 2000 (Thesis) (realistic stars; Np=2000-36000; q=0.001-1; 0.1-30*V_star) Freitag & Benz 2005 (basically the same but published) |
| MS — more compact | Davies, Benz & Hills 1992 (Giant–NS and MS–NS) Davies et al. 1993 (equal-mass MS–WD to compare SPH with grid method, Np up to 27000) Lee, Kim & Kang 1996 (MS–NS, parabolic, d_min>R_MS, M_MS=0.2-0.7 M_sun) |
| Giant — Giant | |
| Giant — more compact | Davies, Benz & Hills 1991 (0.8 M_sun Giant–0.4/0.6 M_sun point mass, parabolic; Np=7000) Davies, Benz & Hills 1992 (Giant–NS and MS–NS) Rasio & Shapiro 1991 Fryer & Woosley 1998, Zhang & Fryer 2001 (He star–BH merger in a binary as GRB engine) Bailey & Davies 1999 (Giant–MS at Galactic center, M_giant=2-8 M_sun, V_rel up to 300 km/s) Lombardi et al. 2006 (Subgiant/Giant–NS as a way to create Ultracompact X-ray binary) |
| WD — WD | Benz, Hills & Thielemann 1989 (parabolic; 0.6–0.6 M_sun + 0.7–0.9 M_sun; Np=5000) Benz et al. 1990 (merger in circular binary) Segretain, Chabrier & Mochkovitch 1997 (mergger in circular binary) |
| WD — more compact | Fryer et al. 1999 (WD–BH in a circularized binary as GRB engine) |
| NS — NS (binary) | Rasio & Shapiro 1992,1994 Centrella & McMillan 1993 (q=1, parabolic; Np=2000/4000) Davies et al. 1994 Rosswog et al. 1999 Faber & Rasio 2000,2002,Faber, Rasio & Justin 2001 (post-Newtonian) Oechslin, Rosswog & Thielemann 2002 (Conform flat approx) Rosswog & Davies 2002, Rosswog & Liebendörfer 2003, Rosswog, Ramirez-Ruiz & Davies 2003, (post-Newtonian; up to 1e6 particles) |
| NS — BH (binary) | Lee & Kluzniak 1995, & Lee, Kluzniak & Wlodzimierz 1999a,1999b, Lee 2000,2001 (Newtonian gravity) Wlodzimierz & Lee 2002 (Quark star-BH!) |
| Collisions featuring binaries | Cleary & Monaghan 1990 (binary — single; n=1.5 polytropes with R~M-1/3; only ~180 part/star) Goodman & Hernquist 1991 (binary — binary; all MS) Davies, Benz & Hills 1993,1994 (binary — single, 3-body runs compared with SPH; binary: NS-MS intruder: NS/WD/MS) Davies et al. 1998 (binary — giant at Galactic center; 4-body checked with SPH runs) Adams, Davies & Sills 2004 (binary — giant in globular clusters) |
A special category is the tidal disruption of a star by a massive black hole, at the center of a galactic nucleus.
See also the reference list for collision simulations with grid methods, below in this page.
15000 SPH simulations of MS-MS collisions
by Freitag and Benz (2004)
 I have put together the files describing the initial condition and outcome of some 15,000 SPH simulations of MS-MS collisions (see Freitag & Benz 2005 and the on-line complements, a 5.2M pdf).
I have put together the files describing the initial condition and outcome of some 15,000 SPH simulations of MS-MS collisions (see Freitag & Benz 2005 and the on-line complements, a 5.2M pdf).
Only simulations included in summary.txt have passed all our tests to sort out “bad” results (poor conservation of energy or angular momentum….) and select the highest resolution simulation when a collision has been simulated with various particle numbers.
These (145 kB) are the initial conditions for all simulations (to be used together with stars.txt to get the stellar masses).
Here you will find the basic information about stellar models (mass and radius) and name of correspond file for internal structure.
The files containing the internal structure of stars can be found here. If you use any of those (except the simple polytrope models), please cite Schaller et al. (1992) , Meynet al al. (1994), Charbonnel et al. (1999).
In this file you have the results in “raw” form: masses, positions and velocities of the star(s) at the end of the collision simulation.
And, to finish with, here you will find a summary of initial conditions and outcomes for all collision simulations.
youtube videos of SPH collisions
Based on the former set of 15000 simulations
On-line resources
SPH in astrophysics is alive and well! I have created a direct (tiny) link to the most recent papers on SPH:
Unfortunately, most web sites concerned with SPH seem to be a bit out-dated, with a lot of dead links. Here is an exception found so far: The on-line course on computational physics, by Franz Vesely, at the University of Vienna, features a chapter on SPH. Unfortunately the chapter seems to have broken images.
Grid and adaptive mesh hydrodynamics (with and without SPH)
The very first simulations of stellar collisions known to us were carried out with low dimension grid codes. To increase the symmetry and decrease the effective dimensionality of the problem, head-on collision between identical MS stars where considered, quite an physically unlikely configuration (Mathis 1967, DeYoung 1968, Seidl & Cameron 1972). Since then, no grid simulation of MS-MS collision has been realized, an unfortunate fact, as this would allow useful comparison with the (quicker) SPH simulations. Most teams have concentrated on collisions involving compact objects.
An interesting addition to adaptive mesh refinement is Octo-Tiger. This code combines grid based adaptive mesh refinement (AMR) methods for simulating hydrodynamical fluids with the fast multipole method (FMM) for computation of the gravitational field. The code uses the differential equations that describe inviscid fluid flow under the influence of its own gravitational field to evolve, in time, the mass, momentum, and energy densities of an astrophysical system. Their approach combines grid based hydrodynamics methods on an octree AMR grid with a specialized version of the FMM. Interestingly, they exploit the idea of Walter Dehnen‘s tree to keep the conservation of energy and angular momentum to machine precision. In their computational paper they give a detailed description of the code.
Also, the code developed by Volker Springel Arepo is a moving-mesh code for hydrodynamical cosmological simulations but it has been used to simulate the collision of two stars in the work of Schneider et al. The Arepo webpage is a bit hidden and difficult to find, but here it is.
As they say, “(it)is a massively parallel code for gravitational n-body systems and hydrodynamics, both on Newtonian as well as cosmological background. It is a flexible code that can be applied to a variety of different types of simulations, offering a number of sophisticated simulation algorithms”. Also, the code was initially developed to combine the advantages of finite-volume hydrodynamics with the Lagrangian convenience of smoothed particle hydrodynamics (SPH). To this end, Arepo makes use of an unstructured Voronoi-mesh which is, in the standard mode of operating the code, moving with the fluid in a quasi-Lagrangian fashion. The fluxes between cells are computed using a finite-volume approach, and additional spatial adaptivity is provided by the possibility to add and remove cells from the mesh according to user-defined criteria. In addition to gas dynamics, Arepo allows for additional collisionless particle types which interact only gravitationally. Besides self-gravity, forces from external gravitational potentials can also be included.
You can clone Arepo here
$git clone git@gitlab.mpcdf.mpg.de:vrs/arepo.git
Here is an incomplete list of grid-based simulations, organized by collision type.
In this table q stands for the mass ratio M_2/M_1; other quantities are defined here.
| Collision type and regime | References |
|---|---|
| MS — MS | Mathis 1967 (1D code, head-on, equal-mass, V_rel=0-400 km/s, nucl. reac. found to be negligible) DeYoung 1968 (1.5-D code, head-on, equal-mass, V_rel=5000 km/s, source of relativistic particles for QSOs?) Seidl & Cameron 1972 (First realistic simul. 2D code, head-on, equal-mass, polytrope n=3, V_rel=0/1.6/3.2 V_star) |
| MS — more compact | Shara & Shaviv 1977,1978 (head-on MS–WD with 2D code with V_rel=300/5700 km/s, M_WD=1 M_sun, M_MS=0.13 M_sun => thermonuclear destruc. of MS star) Shara & Regev 1986 (head-on MS–WD with 2D code with V_rel=0, M_WD=M_star=0.6 M_sun => thermonuclear destruc. of MS star) Regev & Shara 1987 (head-on MS–WD with 2D code with V_rel=2000/6000 km/s, M_WD=0.6, M_star=10 M_sun => destruc. of MS star) Soker et al. 1987 (off-center MS–WD with 3D particle/grid code; V_rel=0, M_MS=0.2, M_WD=0.8 M_sun) Rozyczka et al. 1989 (head-on MS–WD with 2D code, M_WD=0.5 M_sun, M_MS=0.5/1.0 M_sun) Ruffert & Mueller 1990, Ruffert 1992,1993 (MS–WD with PPM; 0.5–0.5 M_sun, various d_min) Davies et al. 1993 (equal-mass MS–WD to compare with SPH) |
| Giant — Giant | |
| Giant — more compact | Tuchman 1985 (Spherical simul of the reaction of a Giant’s envelope to the ejection of its core) Livne & Tuchman 1988 (3-body study of the ejection of a Giant’s core during an interaction with a “point-mass”; 2D, axisym. hydro simul of the envelope during core ejection; V_rel=0-200 km/s) |
| WD — WD | |
| WD — more compact | |
| NS — NS (binary) | Gilden & Shapiro 1984 (head-on with 2D code, Newtonian) Ruffert, Janka & Schaefer 1996, Ruffert et al. 1997, Ruffert & Janka 2001 (PPM, Newtonian + GW emission, various masses & spins) Sewsty, Wang & Calder 2000, Calder & Wang 2002 (Newtonian + GW emission) Shibata & Uryu 2000,2002 (Full GR) |
| NS — BH (binary) | Janka et al. 1999, Ruffert & Janka 1999 (GRB engine? PPM, Newtonian + GW emission) |
A special category is the tidal disruption of a star by a massive black hole, at the center of a galactic nucleus.
See also the reference list for collision simulations in this same page.
Any help to develop this section very welcome…Visit also the page about NS-NS coalescence by Max Ruffert, with nice images and animations.
Miscellaneous
To get an idea about the activities and issues about collisions in cluster dynamics between 2003 and 2004, see the slides presented during the Modest-4 held in Geneva in Jan 2004 for this working group (coll_report_marc_freitag.pdf).